-
 @ThothChildren
@ThothChildren
- 2018.7.22
- PV 1174
反復深化探索
ー 概要 ー
反復深化探索(反復深化深さ優先探索, ID, Iterative deepening depth-first search)は深さを制限した深さ優先探索を最大深さ0から次第に大きくしながら目的のデータが見つかるまで繰り返す探索.深さ優先のメモリの効率性と幅優先探索の完全性、最適性を備え持っているため、深さ優先探索や幅優先探索よりも理論上優れていることが多い.
この章を学ぶ前に必要な知識
条件
- グラフ状で表現されるデータ
効果
- 目的のデータを探索できる
ポイント
- 平均分岐数bと最大深さmで空間計算量もO(bm)
- 完全性と最適性を持った探索が可能
- 最大深さを0から1ずつ大きくしていき、見つかるまで深さ優先探索を繰り返す
- 繰り返す際に一つ前の計算は何も再利用しない
- 深さを深くしたことで増える時間が大きいため、これまでの計算と同じ計算をしてもあまり時間は変わらない
解 説
反復深化探索(反復深化深さ優先探索, ID, Iterative deepening depth-first search)は深さを制限した深さ優先探索を最大深さ0から次第に大きくしながら目的のデータが見つかるまで繰り返す探索.
手法
1. ルートノードより最大深さdを0として探索を開始.
2. 現在の最大深さdに1を加えて、深さ優先探索を行う.
3. 2.で見つからなければ再度2.を実行.見つかるまで繰り返す.
深さ優先のメモリの効率性と幅優先探索の完全性(解があったら必ず見つかる)、最適性(最も浅い解が見つかる)を備え持っているため、深さ優先探索や幅優先探索よりも理論上優れていることが多い.
毎回最大深さを1ずつ加えていき再度深さ優先探索を実行するが、このとき一つ小さい最大深さのときの深さ優先探索と同様なことを行っていて無駄に思われる.しかし実際は次の深さの探索を行うことによって増える時間の方が大きいため、繰り返し同じような探索をしている時間は大して無駄になっていない.
空間計算量は深さ優先探索を用いているため、ほぼ同様に平均分岐数bと解の深さdからO(bd)と分かる.
また、時間計算量はO(b^d)となる | 反復深化探索について |
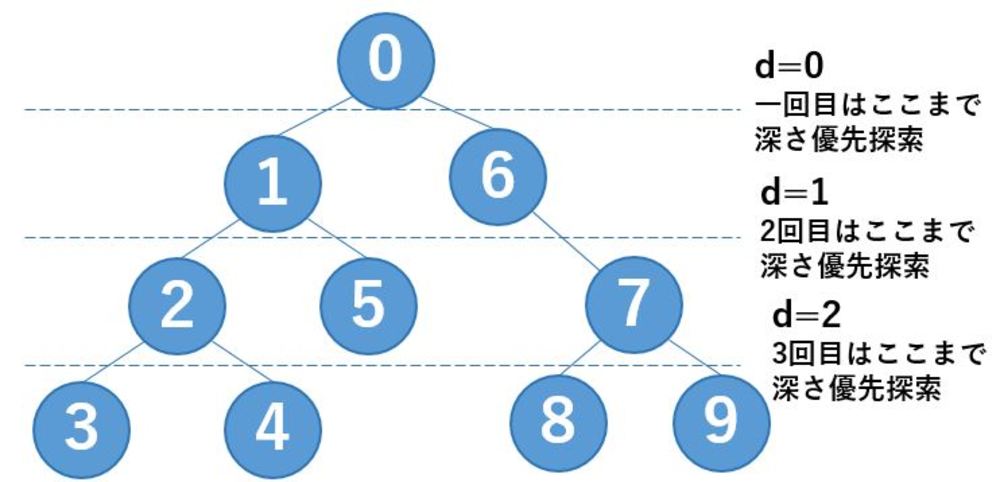
 | 反復深化探索の様子.
何度も深さ優先探索を繰り返す.
図のノード番号はd=3のときのもの |
この章を学んで新たに学べる
Comments


