-
 @ThothChildren
@ThothChildren
- 2018.7.22
- PV 200
幅優先探索
ー 概要 ー
幅優先探索はグラフデータの中でスタートのデータから浅いデータから探索し、見つからなければ更に深いところで次の候補を探していく探索.今まで見てきたデータを保持するため空間計算量が大きく、頂点数VでO(V)、または深さdと平均分岐数bを用いてO(b^d)と記述できます
この章を学ぶ前に必要な知識
条件
- データがグラフ状態で表現される
効果
- グラフデータの中から目的のデータを見つける
ポイント
- データの探す候補はFIFO(First In First Out)のキューに加えていく
- 見てきたデータは全て保持しておく必要がある
- 空間計算量はO(V)
- 最悪時間計算量はO(V+E)
解 説
幅優先探索はグラフデータの中でスタートのデータから浅いデータから探索し、見つからなければ更に深いところで次の候補を探していく探索.
探索する候補のノードはFIFO(First In First Out)なデータ構造のキューに蓄えていきます.
幅優先探索:手法
1. はじめのルートノードから次の深さの子ノードをキューに入れる
2. キューに入っているノードを取り出して、探しているものか判定. 取り出したノードに子ノードがあればキューに追加
3. キューがなくなるか探しているノードが見つかるまで2.を繰り返す
頂点の数をV、エッジの数をEとして、時間計算量はO(V+E)になります.
今まで見てきたデータを保持するため空間計算量が大きく、頂点数VでO(V)、または深さdと平均分岐数bを用いてO(b^d)と記述できます. | 幅優先探索 |
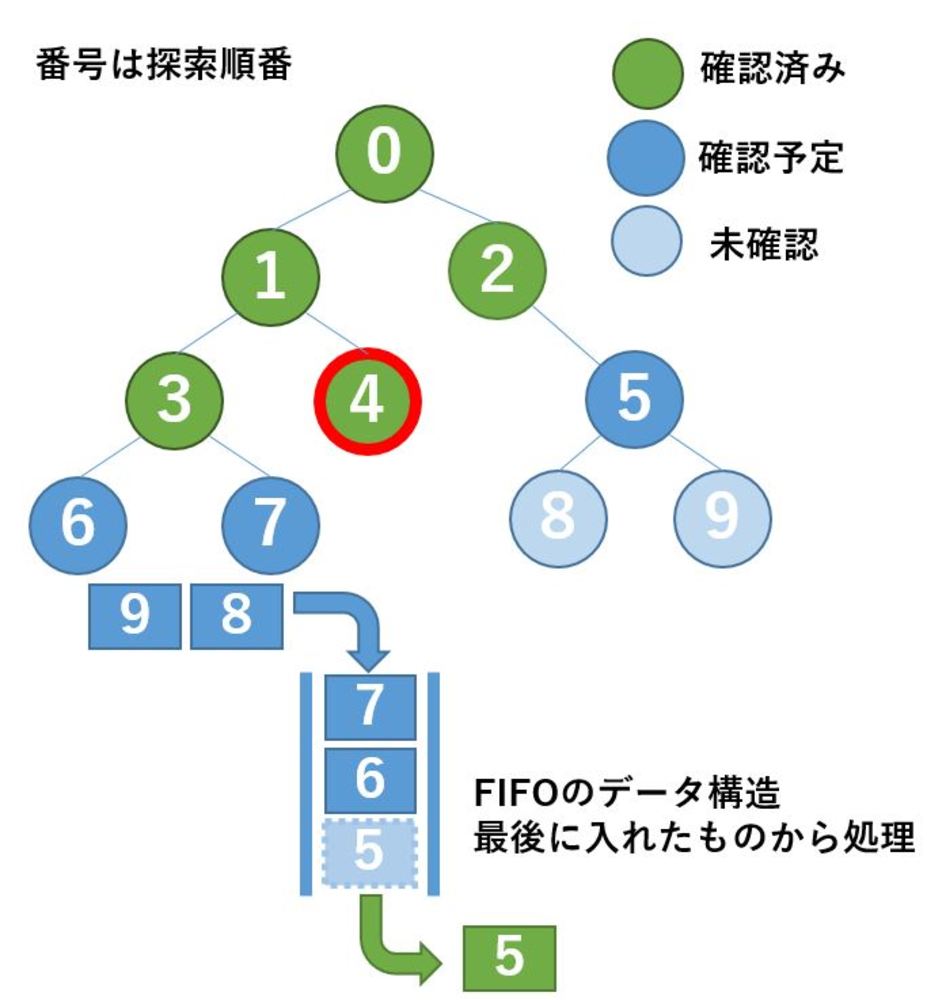
 | ノードの番号がこの探索で確認していく順番です.
確認すべきノードを見つけたらそれをFIFOのキューに加えていきます.
ここでは0,1,2,3,4までのノードを確認し終えていて、次は5を取り出すところです.
5を取り出す前まではキューの中には5,6,7がありましたが、5を取り出すことで、6,7のみとなり、また5の子ノードである8,9が追加されます.
そのため5を確認し終えたところでキューの中には9,8,7,6が入っている状態になります. |
この章を学んで新たに学べる
Comments


