-
 @ThothChildren
@ThothChildren
- 2018.7.22
- PV 340
二分探索
ー 概要 ー
二分探索はデータを持つ配列やリストをあらかじめある大きさを基準にソートしておき効率的に探索する手法です.配列の真ん中の値を見てそれが探したい値より大きいか小さいかで対象を絞りこんでいきます.計算量はO(log(n))になります.
この章を学ぶ前に必要な知識
条件
- データが配列に入っている
- 配列のデータが全てソートされている
- 同一の値はないとする
効果
- 効率的に要素を探索
- 計算量はO(log(n))
ポイント
- データをあらかじめソートする必要があるため、そちらの処理時間もかかる
- 毎回候補が半分ずつになっていく
- 2^n個のデータがあればn回の比較で探索完了. 逆にN個のデータあればlog(N)回で探索完了.
解 説
二分探索はデータを持つ配列やリストをあらかじめある大きさを基準にソートしておき効率的に探索する手法です.
配列の真ん中の値を見てそれが探したい値より大きいか小さいかで対象を絞りこんでいきます.
二分探索:手法
1. あらかじめ配列のデータを比較したい値の種類でソートしておく.
2. 候補の真ん中のデータを取り出し、探している値と比べて大きいか小さいかを判定
3. 2.で大きければ真ん中のデータより大きい候補に絞込み、小さければ真ん中のデータより小さい候補に絞込み
4. 3.で絞り込まれた候補に対して再度2.を行い、見つけたいデータになるまで繰り返します.
一度に候補が半分になるため、データが2^n個あった場合はn回でデータを見つけ出すことができます.逆にデータがN個あったするとlog(N)回でデータを見つけ出すということです.
そのため、計算量はO(log(N))とわかります. | 二分探索について |
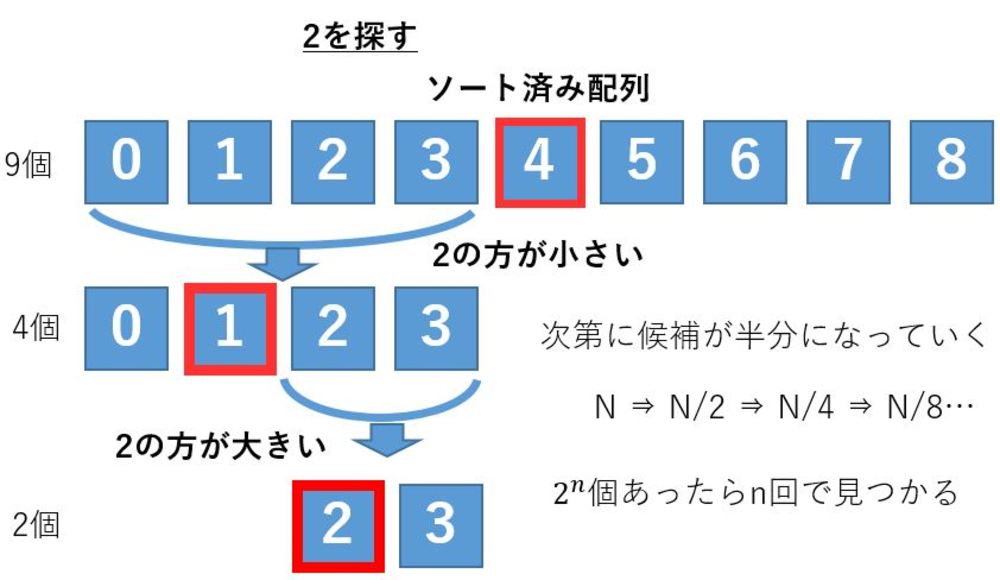
 | ソートがされている配列の中から2を見つけ出す例です.
まず配列の真ん中の4と比較してそれより左側にデータがあるとわかります.
左側の0~3の中で1を真ん中のデータとして取り出して比較します.すると今度は1より右側にあるとわかります.
次に2,3のうち2を選択して比較します.一致しているためこれで探索を終了します.
この場合全部で9個ありlog2(9)≒3回比較を行えばデータを見つけられることがわかります. |
二分探索は現実で対象のファイルデータを探すときなどでも使えます.
ある時点でおかしくなったファイルを探すようなときに
先頭からしらみつぶしに探すのではなく、時系列順でファイルをソートして、見つけたいデータかどうかを効率よく探していくことができます. | 二分探索の実用的な使い道 |
この章を学んで新たに学べる
Comments


