-
 @ThothChildren
@ThothChildren
- 2018.7.22
- PV 165
自己組織化探索
ー 概要 ー
自己組織化探索はデータを含む配列やリストなどから線形探索のようなしらみつぶしの探索をした後に見つけ出した要素を配列から削除して先頭に挿入する探索アルゴリズムです.これは複数回探索を行うことで効率的に探索ができるようになっていきます.探索するデータに偏りがありデータによって頻繁に探索されることが前提です.
この章を学ぶ前に必要な知識
条件
- データが配列に格納されている
- 探索する要素に偏りがあり、頻繁に探索される要素がある
- 線形探索より効率的になるには回数が増える必要あり
効果
- 複数回探索することで目的のデータを効率的に探索する
ポイント
- 探索の計算時間はO(n)
- 見つけ出した要素を配列から削除して先頭に持ってくる
解 説
自己組織化探索はデータを含む配列やリストなどから線形探索のようなしらみつぶしの探索をした後に、見つけ出した要素を配列から削除して先頭に挿入する探索アルゴリズムです.
探索するデータに偏りがありデータによって頻繁に探索されることが前提です.即ち例えば"0"を一度探索されたら近いうちに再度"0"で探すと先頭に"0"を置いているので直ぐに見つけることができます.そのため効率的になっています.
自己組織化探索:手法
1.配列の先頭から目的のデータを探す.
2.見つけた目的のデータを配列から削除して、先頭に移動
これは複数回探索を行うことで効率的に探索ができるようになっていくもので、一回しか行われない探索では線形探索と同じです. | 自己組織化探索について |
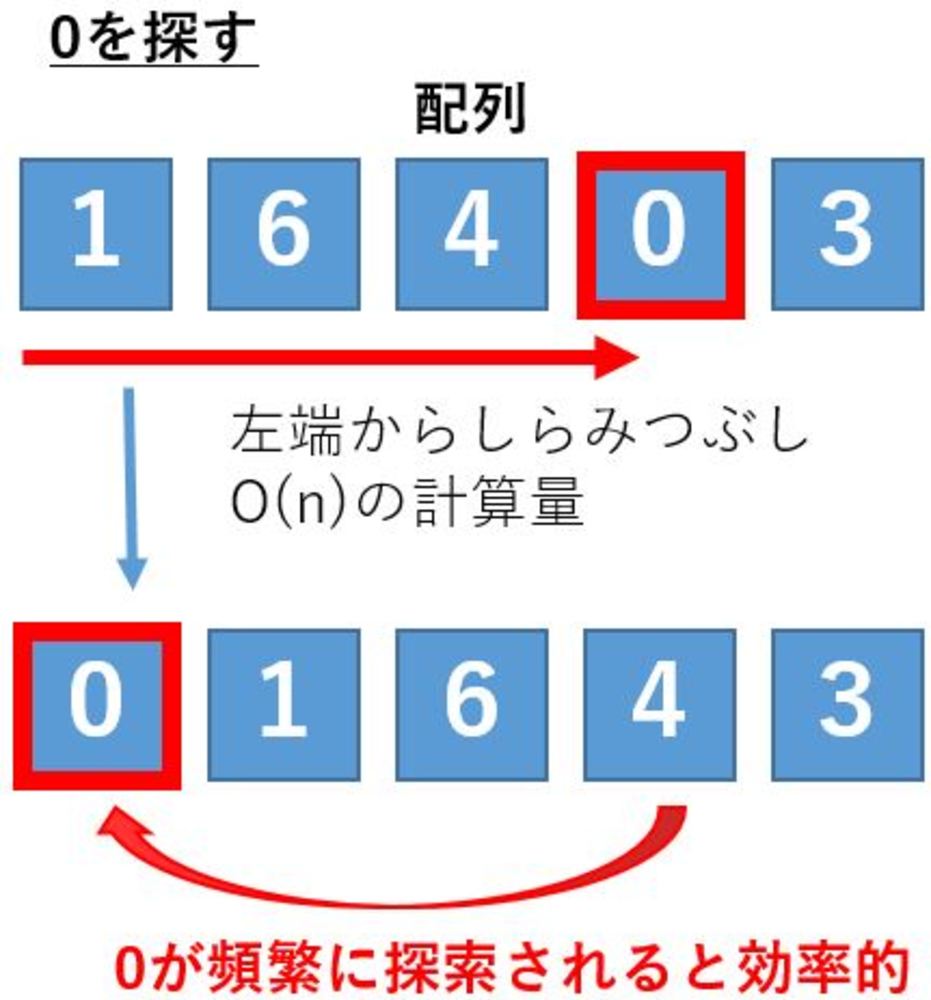
 | 自己組織化探索の説明図
0を探している例.線形探索と同じように配列の先頭から一つずつ比較しながら目的のデータを探します.
データを見つけ出した後に、元の場所から削除して先頭に持って行ってます. |
頻繁に探索されるデータがあった場合に配列の先頭に持ってくる手法を紹介しました.
しかし、逆に一度探索されたらもう探索されないデータがある場合は逆に先頭ではなく末尾に加えます.
そのようにすると次の探索で不要な比較を減らすことができます. | 自己組織化探索その他について |
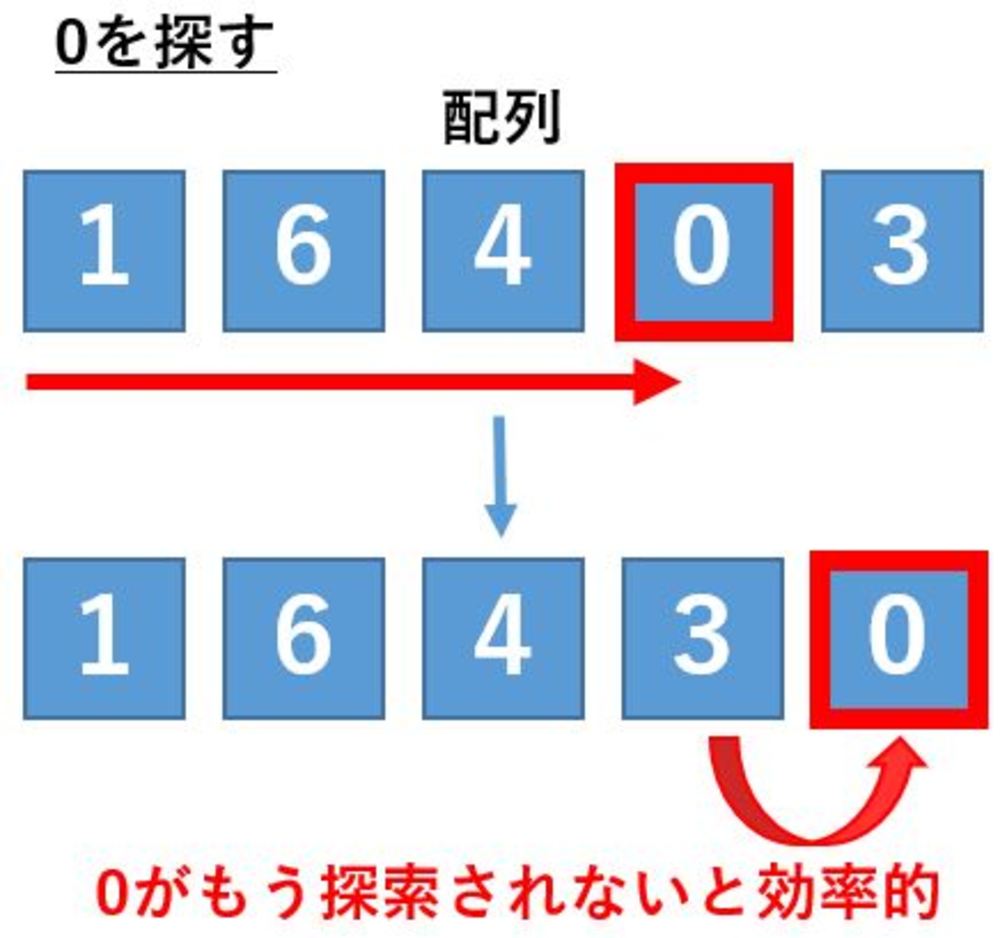 | 上記と同様に今度はもう探索されない要素がある場合は、末尾に移動させます.
次回以降この要素を無駄に比較しないで済みます. |
この章を学んで新たに学べる
Comments


