姿勢変換行列

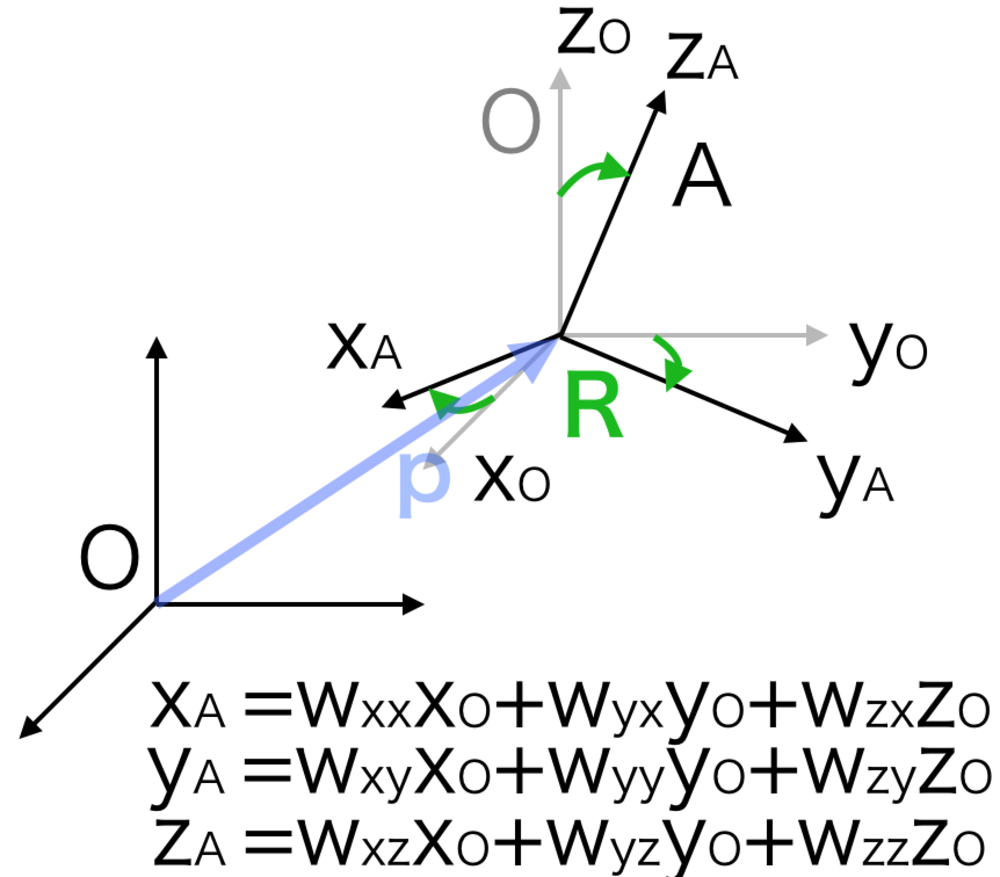
姿勢変換行列はある座標系Oを基準に座標系Aの姿勢を表現した行列で回転行列とも呼ぶ.(以下Rと表現する) 姿勢変換行列Rの各列ベクトルは基準の座標系Oの軸の単位ベクトルを用いて座標系Aの軸の単位ベクトルを表現したときの重みにあたる. $$R_{OA} = ( e_{x_A}, e_{y_A}, e_{z_A} ) $$ $$ e_{x_A} = w_{x_Ax}e_{x_O}+w_{x_Ay}e_{y_O}+w_{x_Az}e_{z_O} = \left( \begin{array}{c} w_{x_Ax} \\ w_{x_Ay} \\ w_{x_Az} \end{array} \right)$$

次に座標系Aとは別に座標系Bがあるとする. 姿勢変換行列OAと姿勢変換行列OBを使って、姿勢変換行列ABが記述できることを導く. まず先に記述した\(e_{x_A},e_{y_A},e_{z_A}\)と\(e_{x_B},e_{y_B},e_{z_B}\)を用いて姿勢変換行列ABを記述する. 例えば\(e_{x_B}\)を座標系Aの軸の単位ベクトル\(e_{x_A},e_{y_A},e_{z_A}\)で表現できればよいが、これは\(e_{x_B}\)の座標系Aの軸への正射影をすることで簡単に求められる.すなわち内積をとることになる. $$ R_{AB}=\begin{eqnarray} \left( \begin{array}{ccc} e_{x_A}^Te_{x_B} & e_{x_A}^Te_{y_B} & e_{x_A}^Te_{z_B} \\ e_{y_A}^Te_{x_B} & e_{y_A}^Te_{y_B} & e_{y_A}^Te_{z_B} \\ e_{z_A}^Te_{x_B} & e_{z_A}^Te_{y_B} & e_{z_A}^Te_{z_B} \end{array} \right) \end{eqnarray} $$ 分解すれば、 $$ \begin{eqnarray} R_{AB} &=& \left( \begin{array}{c} e_{x_A}^T \\ e_{y_A}^T \\ e_{z_A}^T \end{array} \right) \left( \begin{array}{ccc} e_{x_B} & e_{y_B} & e_{z_B} \end{array} \right)\\ &=& \left( \begin{array}{ccc} e_{x_A} & e_{y_A} & e_{z_A} \end{array} \right)^T \left( \begin{array}{ccc} e_{x_B} & e_{y_B} & e_{z_B} \end{array} \right)\\ &=& R_{OA}^T R_{OB} \end{eqnarray} $$ と記述できる. さらに、逆の\(R_{BA}\)を考えてみるとこれは、 $$ \begin{eqnarray} R_{BA}&=& \left( \begin{array}{ccc} e_{x_B}^Te_{x_A} & e_{x_B}^Te_{y_A} & e_{x_B}^Te_{z_A} \\ e_{y_B}^Te_{x_A} & e_{y_B}^Te_{y_A} & e_{y_B}^Te_{z_A} \\ e_{z_B}^Te_{x_A} & e_{z_B}^Te_{y_A} & e_{z_B}^Te_{z_A} \end{array} \right) \\ &=& \left( \begin{array}{ccc} e_{x_A}^Te_{x_B} & e_{x_A}^Te_{y_B} & e_{x_A}^Te_{z_B} \\ e_{y_A}^Te_{x_B} & e_{y_A}^Te_{y_B} & e_{y_A}^Te_{z_B} \\ e_{z_A}^Te_{x_B} & e_{z_A}^Te_{y_B} & e_{z_A}^Te_{z_B} \end{array} \right)^T \\ &=& R_{AB}^T \end{eqnarray} $$ とわかる.すなわち姿勢変換行列を転置行列にしたものが元の姿勢変換行列の逆変換になるということがわかる.それを用いると, $$ \begin{eqnarray} R_{AB}&=&R_{OA}^T R_{OB}\\ &=&R_{AO}R_{OB} \end{eqnarray} $$ と記述できることがわかる.これから姿勢変換行列同士はそれらを以下のようにチェーンルール(連鎖律)に従って変換することで容易に変換できることがわかる. $$R_{OX} = R_{OA}R_{AB}\dots R_{WX} $$

姿勢変換行列Rは直交行列であるため以下の性質が常に成り立つ. $$RR^T=E$$ $$R^T=R^{-1}$$ $$detR=1$$