同次変換行列

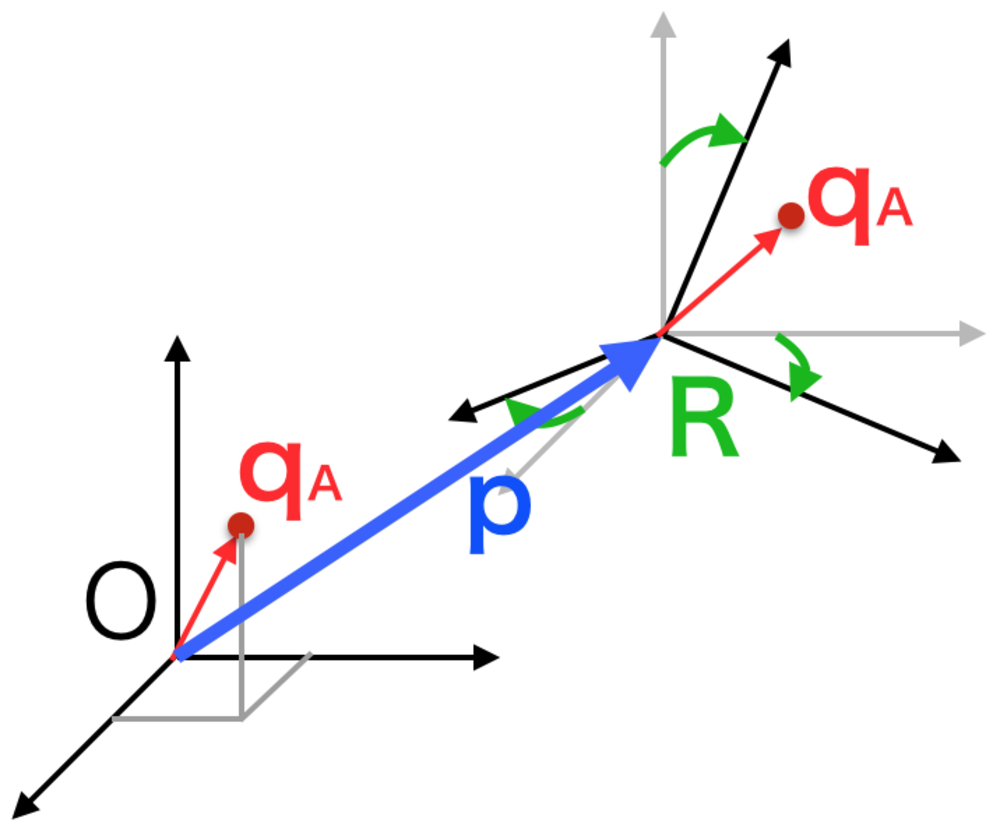
基準の原点座標系Oにおいて、ある座標系AがありそのqAの位置にA座標系に固定された点Qがあるとする. 座標系Aを原点座標系Oでpだけ移動して、原点座標系Oに対してRだけ回転させたときを考える. そうすると、座標系と一緒に移動する点Qの原点座標系における位置qOは以下のように書ける. $$q_O=p_O + R_{OA}q_A$$ これを行列の形で記述すれば、以下の形で表現できる. $$ \left( \begin{array}{c} q_O \\ 1 \end{array} \right) = \begin{eqnarray} \left( \begin{array}{ccc|c} & & & \\ & R_{OA} & & p_O \\ & & & \\ \hline 0 & 0 & 0 & 1 \\ \end{array} \right) \end{eqnarray} \left( \begin{array}{c} q_A \\ 1 \end{array} \right) =H_{OA} \left( \begin{array}{c} q_A \\ 1 \end{array} \right) $$ この\(H_{OA}\)を同次変換行列と呼ぶ.この行列は座標系Aの位置と姿勢の情報を持っており、座標系に剛体があれば、剛体の位置と姿勢を持っていることになる.

同次変換行列を複数掛け合わせることによって、連鎖したような座標変換を表現することができる. 例えば、先の座標系Aの中で\(q_A\)が実は別の座標系B内の固定点Xをすでに移動して回転してA座標系で算出したものと考えれば $$\left( \begin{array}{c} q_A \\ 1 \end{array} \right) = H_{AB} \left( \begin{array}{c} q_B \\ 1 \end{array} \right) $$ の形で表現できるはず. これを初めの式に代入すれば、 $$\left( \begin{array}{c} q_O \\ 1 \end{array} \right) = H_{OA} H_{AB} \left( \begin{array}{c} q_A \\ 1 \end{array} \right)= \begin{eqnarray} \left( \begin{array}{ccc|c} & & & \\ & R_{OA}R_{AB} & & R_{OA}p_A+p_O \\ & & & \\ \hline 0 & 0 & 0 & 1 \\ \end{array} \right) \end{eqnarray} \left( \begin{array}{c} q_A \\ 1 \end{array} \right) $$ と記述できる.\(R_{OA}R_{AB}\)は回転行列同士の積なので回転行列になります.位置座標も同様に位置座標を表します. そのため上記は $$\left( \begin{array}{c} q_O \\ 1 \end{array} \right) = H_{OB} \left( \begin{array}{c} q_A \\ 1 \end{array} \right)$$ と書き直すことができ、X座標系までの座標変換を行っていれば、 $$H_{OX} = H_{OA} H_{AB} \dots H_{WX}$$ Hは直行行列ではありません.

Hが以下のように書けるとすると $$H =\begin{eqnarray}\left( \begin{array}{ccc|c} & & & \\ & R& & p \\ & & & \\ \hline 0 & 0 & 0 & 1 \\ \end{array}\right)\end{eqnarray}$$ Hの逆行列は常に以下のように記述できる. $$H^{-1} =\begin{eqnarray}\left( \begin{array}{ccc|c} & & & \\ & R^T& & -R^Tp \\ & & & \\ \hline 0 & 0 & 0 & 1 \\ \end{array}\right)\end{eqnarray}$$ 確認するために積を計算すると $$HH^{-1} =\begin{eqnarray}\left( \begin{array}{ccc|c} & & & \\ & RR^T& & -RR^Tp+p \\ & & & \\ \hline 0 & 0 & 0 & 1 \\ \end{array}\right)\end{eqnarray} =E$$ \(RR^T\)は回転行列は常に直交行列で、直交行列は常に以下の関係が成り立つため、上記の式が単位行列となる. $$RR^T = E $$