-
 @ThothChildren
@ThothChildren
- 2018.7.7
- PV 1983
多変数関数の極大極小を判定したい
ー 概要 ー
多変数関数を入力に一変数を出力する関数に対してある点が極大値になっているか極小値になっているか鞍点になっているかを判定する方法についてまとめています.ヘッセ行列を用いて判定します.
この章を学ぶ前に必要な知識
条件
- 多変数を入力に1変数出力の二階微分可能な関数
効果
- 二変数の場合、ヘッセ行列の行列式が負なら鞍点、行列式が正且つfのx(またはy)の二階微分が正なら極小、負なら極大
- ヘッセ行列の行列式が0のときは、極大値なのか極小値なのか鞍点なのか全く違うものか一切の判断がつかない
- 多変数で一般化した場合、ヘッセ行列が正定値行列なら極小値、負定値行列なら極大、固有値に正も負も(0ではない)含まれるとき鞍点、それ以外は何もでもない
解 説
多変数関数の極大極小を判定する方法についてまとめます.
ここで紹介するのは、ヘッセ行列による極大値極小値鞍点判定です. | 多変数関数の極大極小を判定したい |
ヘッセ行列に関する解説は右参照.
簡単にいえば、f(x_1,x_2,...x_n)をx_1,x_2....x_nで二階微分して行列にしたもの | ヘッセ行列 |
極値は多変数関数\(f\)を一階微分してそれが0になるような入力\(x\)を求めると 停留点を得ることができます.
$$\nabla f(\boldsymbol{x})=\boldsymbol{0}$$
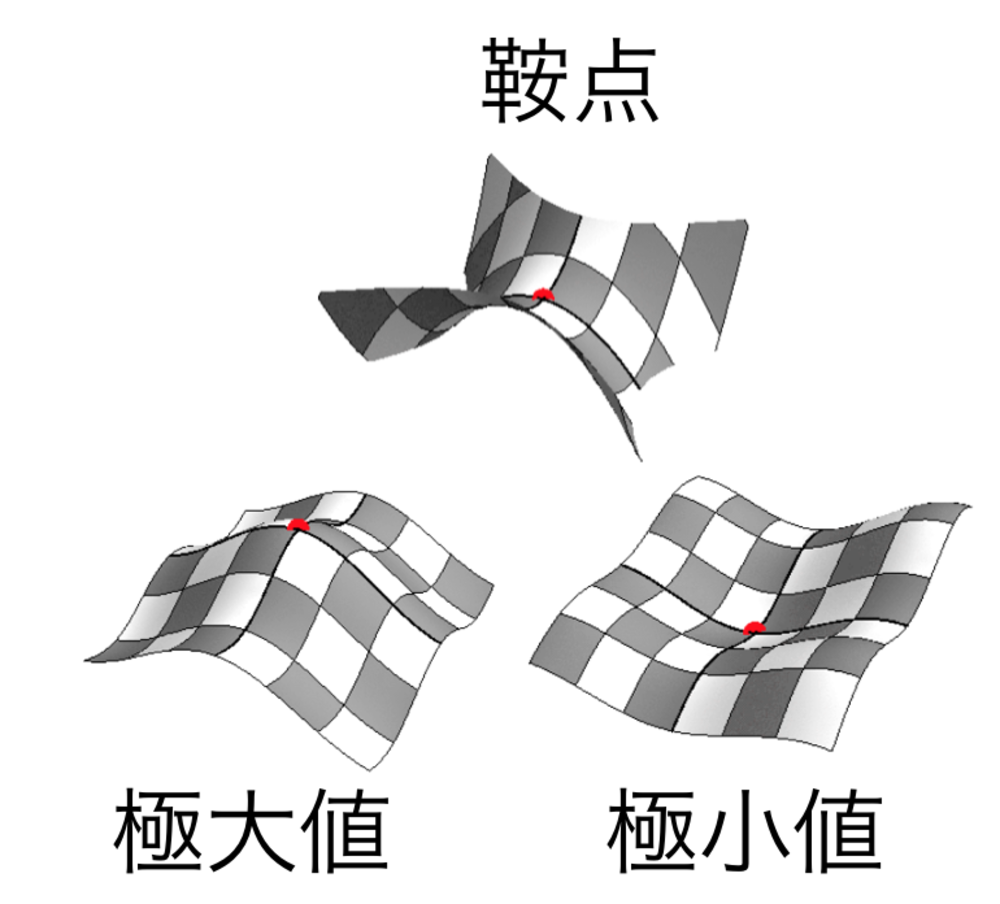
この停留点は以下のどれかです.
・極小値:局所的に最小になっている停留点
・極大値:局所的に最小になっている停留点
・鞍点 :極値にはなっていない点
| 極値簡単な整理 |
1.ヘッセ行列で極値か判定 | |
多変数関数の場合をまとめます.
・極小値 : ヘッセ行列が正定値行列(すべての固有値が正)
・極大値 : ヘッセ行列が負定値行列(すべての固有値が負)
・鞍点 : ヘッセ行列の固有値が正または負の両方を含んでいる
・それ以外はなんとも言えない. | ヘッセ行列による判定まとめ
多変数関数の場合 |
二変数の場合の特殊な場合をまとめます.
・極小値 : ヘッセ行列の行列式が正 且つ fのxまたはyによる二階微分が正
・極大値 : ヘッセ行列の行列式が正 且つ fのxまたはyによる二階微分が負
・鞍点 : ヘッセ行列の行列式が負
・ヘッセ行列の行列式が0のときは、何も判定できない | 二変数の場合の
ヘッセ行列による判定まとめ
|
\(f(x_1, x_2)=(3x_1 + 2)(x_1-3)(x_2 +7)(2x_2-4) \)のとき
$$\begin{eqnarray}
\nabla f(x_1, x_2) &=& \boldsymbol{0}
\end{eqnarray}
$$
より
$$\begin{eqnarray}
\frac{ \partial f(x_1, x_2)}{\partial x_1} &=& (6x_1-7)(x_2+7)(2x_2-4)=0 \\
\frac{ \partial f(x_1, x_2)}{\partial x_2} &=& (3x_1+2)(x_1-3)(4x_2+10)=0
\end{eqnarray}
$$
から
$$(x_1, x_2) = (\frac{7}{6}, -\frac{5}{2} ),(3, 2),(3,-7),(-\frac{2}{3}, 2),(-\frac{2}{3}, -7)$$
が停留点としてあげられる.
ここで、二階微分したヘッセ行列を求めると
$$H= \begin{pmatrix}
6(x_2+7)(2x_2-4) & (6x_1-7)(4x_2+10) \\
(6x_1-7)(4x_2+10) & 4(3x_1+2)(x_1-3)
\end{pmatrix}$$
なので、例えば\(x=(\frac{7}{6}, -\frac{5}{2})\) のときヘッセ行列は,
$$H= \begin{pmatrix}
-243 & 0 \\
0 & -\frac{121}{3}
\end{pmatrix}$$
となり、Hの行列式を求めると\(det(H) = 9801 > 0\)で\(fxx=-243 < 0\)なので\(x=(\frac{7}{6}, -\frac{5}{2})\)において、極大値とわかる. | 二変数の場合のヘッセ行列の判定例 |
この章を学んで新たに学べる
Comments
Reasons
知識: ヘッセ行列
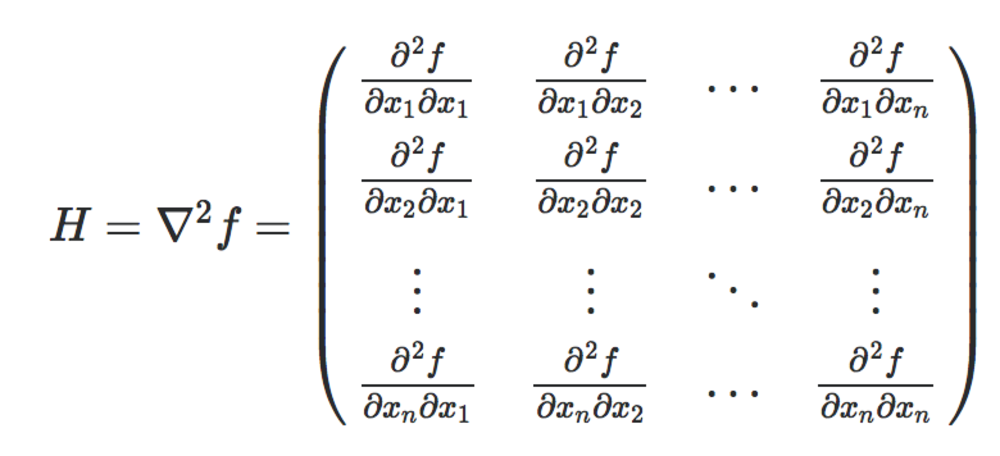
多変数関数f(x_1, x_2, x_3....)のような関数を各x_1, x_2...で二階微分を行い行列としたものをヘッセ行列という.極値の判定やニュートン法における近似解導出に用いられる


