-
 @ThothChildren
@ThothChildren
- 2018.6.28
- PV 764
シンプルに画像に円を描画したい
ー 概要 ー
ピクセル画像上に円を描く方法について紹介します.線の描画ではブレセンハムのアルゴリズムですが、こちらも同様な考え方で行われるmidpoint circle アルゴリズムによるものです.

この章を学ぶ前に必要な知識
条件
- 円の位置と半径
効果
- ピクセル画像で円を近似したものを描画
ポイント
- 円の8分の一を描いてそれを反転やコピーして円にする
- ブレゼンハムのアルゴリズムと同様の発想
解 説
ピクセル画像に単純な円を描画する方法についてまとめています.
ここで紹介するものはブレゼンハムのアルゴリズムと同様な発想のMidpoint Circle Algorythmです.
| シンプルに画像に円を描画したい |
線の描画に関しては右で記載しています.
こちらはブレゼンハムのアルゴリズムです. | シンプルに画像に線を描画したい |
まず円の8分の一を考えます.
下の図のように半径をrとしたときに、(r,0)から円を書き始めて、
(r,r)になるまでピクセルを埋めていきます.
このときにyは必ず1ずつ増えますが、xは0または1減らす(2以上だと線が途切れてしまう)ことがわかります.
そのためxを増やさないままか1増やすかの選択を繰り返し、(r,r)になるまで点を打っていきます.
以上でアルゴリズムは完成です.とてもシンプルで実装も容易です.0のままか1を増やすかは、どちらがよりx^2+y^2=r^2の形に近くなるかで判定すればよいです.(rの近いほう)
平方根を行うと遅くなるので、平方根を使わないで比較をします. | Midpoint Circle Algorythmについて |
 | Midpoint Circleアルゴリズムの概要図
半径をrとして、中心は原点にあるとします.
実際に描画するときには中心のオフセット分を足し合わせればよいです. |
次の点を0を減らすか維持するかを決めるにあたり、前回の座標が\((x_i,y_i)\)だったときに、どのような判定式になるかを計算します.
rとx,yのユークリッド距離の誤差を与える関数をerrとして、\(y_i\)は常に1増やすことに注意すると
$$err(x_i-1, y_i+1) < err(x_i, y_i+1)$$
のように記述することができます.
この不等式を解いていくと最終的に、以下が導かれます.
$$2err(x_i, u_i) + (2y_i+1) + (1-2x_i) >0$$
すなわち上記の式で判定を行えます.この数式においては、整数値の掛け算と足し算のみしか含まれないので、高速に判定を行うことができます. | Midpoint Circle Algorythmの整数値の判定 |
この章を学んで新たに学べる
Comments
Reasons
知識: シンプルに画像に線を描画したい
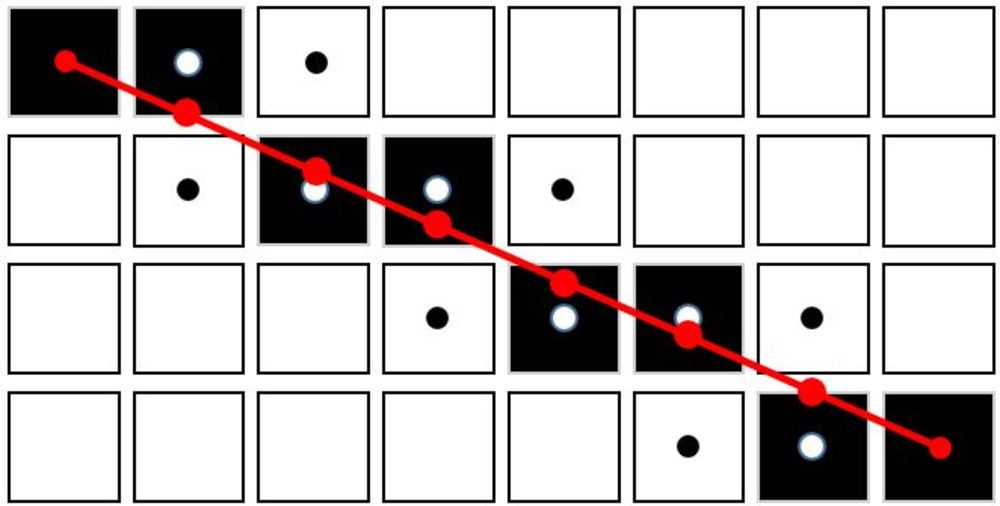
シンプルな方法を用いて画像に線を描画する方法についてまとめます.高速性と正確性の観点からブレセンハムの線描画アルゴリズムが有名で、頻繁に使用され、また様々なハードウェア実装もされています.


