-
 @ThothChildren
@ThothChildren
- 2018.5.26
- PV 184
データの真ん中ぐらいの特徴を知りたい
ー 概要 ー
データ全体の真ん中の値がどれくらいなのかを知りたいときに使用することができる技術についてまとめます.

この章を学ぶ前に必要な知識
条件
- 複数のデータを持つ1次元のデータ列
効果
- データの真ん中ぐらいの特徴量を得る
ポイント
- 複数の真ん中ぐらいの値の取得方法がある
- 分布の形でふさわしい特徴量は異なる
- 特徴量によってノイズに対する耐性や計算時間が異なる
解 説
1次元のデータ列の真ん中ぐらいの値を知りたいときの計算方法についてまとめます.
どんな計算方法で真ん中ぐらいの値を出すかによって得られる情報の質は異なってきます.
どの特徴量を選ぶべきかは
・何を知りたいのか
・分布の状況がどうなっているか
・ノイズはどのように出ているのか
を主に気にする必要があります. | データの真ん中ぐらいの特徴を知りたい |
それではまず真ん中ぐらい(average)の特徴量を簡単に列挙します.
平均値(mean)
全体を足し合わせてその数で割ったもの.よく使用されるが大きな外れ値に影響を受けやすい.しかし全体的な特徴を示す点でやはり有用.分布が偏っているときには不適.
中央値(median)
全体を大きさの順に並び替えてその列の順番として最も真ん中を選択する.これによってたとえ大きな値、小さな値の外れ値が出てきても大きく影響を受けることはない.分布が偏るときにもある程度適切な値を算出.数値のようなデータの大小が線形に決まっているものにのみ適用可能.ソートするためデータ量によっては時間が若干かかる.
最頻値(mode)
最も値が多い値を採用する.多くのデータある中でどの値が最も多いかを見るとデータ全体の一つの特徴を見ることができる.あらかじめどれくらいの範囲を一つのグループとするかbinサイズを決める必要がある.またデータが少ないときにはあまり有用な値にならない.この特徴量はたとえデータが線形に並べられない「文字列」等でも使用することができる.
トリムミーン(Trimmed mean)
ノイズが多い上位と下位数パーセントをあらかじめ切り落とした状態で平均を取る.これによって通常のmeanよりノイズに強い値になる.ソートするためデータ量によっては時間が若干かかる.
Winsorized mean
トリムミーンにさらに重みを加えたような値を出力する.Winsorized meanは上位と下位数パーセントの値をそれに該当しなかった値に置き換えて平均を算出します.他の特徴量よりさらにロバストな平均値(average)になります.ソートするためデータ量によっては時間が若干かかる.
ミッドレンジ(midrange)
(通常外れ値になりやすい)最大値と最小値の値を2で割ったもの.
ノイズに非常に弱くメリットもないため使わないほうが無難.
ミッドヒンジ(midhinge)
データ全体の上から1/4にあたる値と下から1/4にあたる値の平均したもの.分布が綺麗にシンメトリックであれば中央値と近い値になる.
Trimean(日本語不明)
データ全体の上から1/4にあたる値と下から1/4にあたる値にそれぞれ重みを1を掛け合わせ、中央値に重みを2を掛け合わせて足し合わせたもの.人工統計の平均において効率的に算出することができる.たった3点を得るだけでおおよその値を見積もることができる.適切に計算するには分布がシンメトリックで対照的でデータ量が多いほうがよい.ソートするためデータ量によっては時間が若干かかる.
| データの真ん中ぐらいの特徴量を列挙 |
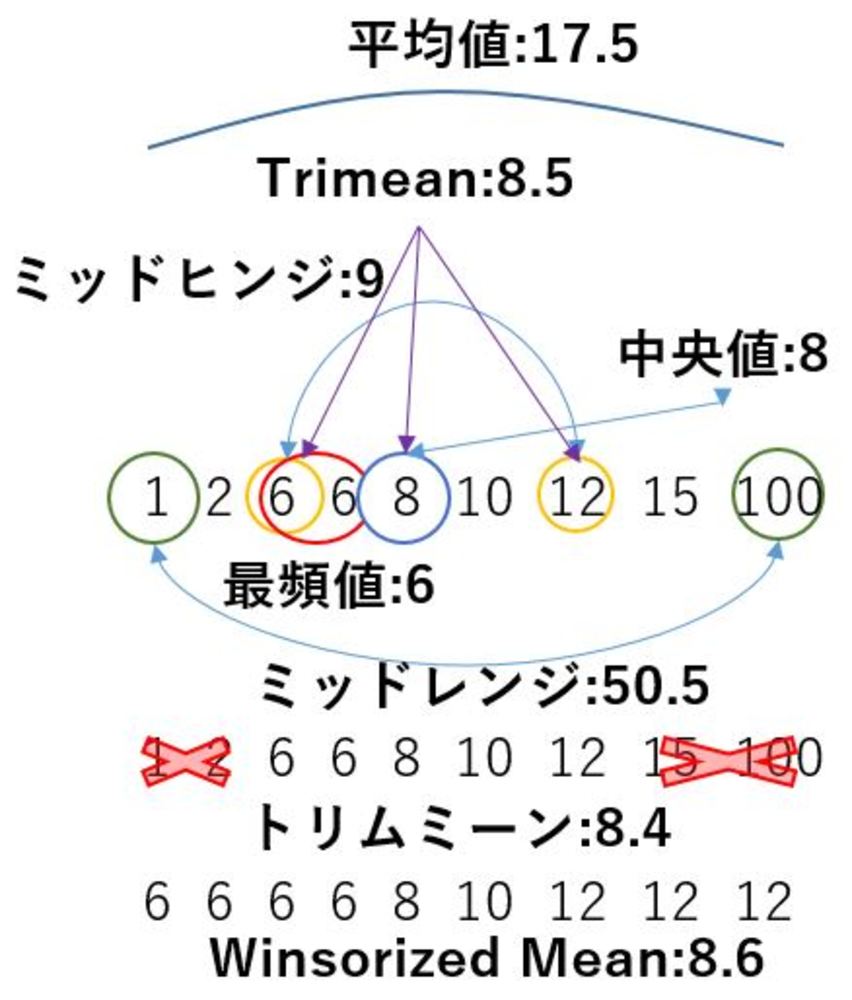 | 各特長量の値の例 |
この章を学んで新たに学べる
Comments


