矩形領域同士の一致度が欲しい

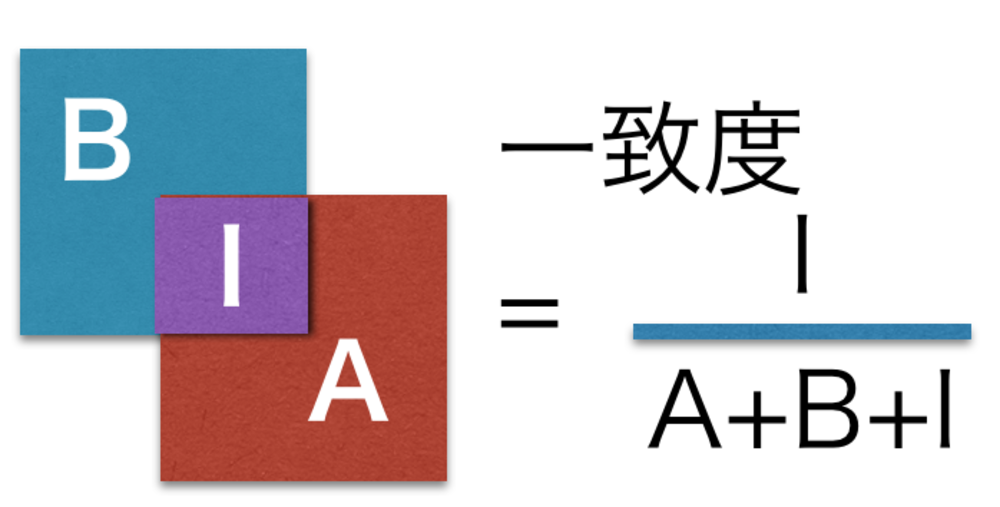
機械学習などで物体領域を推定したときに、推定した物体領域がどれほど正解と正しいかなどは、一見どう評価するか悩みますが、すぐに重なり具合で良いことがわかると思います. 必ずしても機械学習じゃなくても、矩形領域の一致度を求められることはメリットがありそうです. 今回ここで紹介する類似度は、集合の類似度で用いるJaccord類似度, Dise類似度,類似度です.

どの特徴量を使用するにしても先に ・重なっている部分の面積(I) ・重なっていない部分の面積(A) ・重なっていない部分の面積(B) を算出する必要があります. これらは矩形の角の頂点がわかっていれば簡単に求めることができます.重ねっている領域に関しても各領域から頂点を一つずつ借りてくれば簡単に求められます.

それでは上記の面積の値があることを前提に各類似度を求めます.どれが最も優れているということはなく、各特性に沿ってもっとも利用するにあたって適合する類似度を使用すれば問題ありません.

最も有名な集合の類似度.直感的な類似度で、共通の面積が全体のどれくらいを示すかの割合です. 片方を含んでいる場合は1になりません.重なりがなければ0, 完全一致で1になります.

$$Jaccard類似度 = \frac{ I }{ I + A + B }$$

Dise類似度はもともとバイナリデータへ適用することを想定して作られた.Jaccard類似度とほとんど効用は変わらず、お互いの類似度を用いてお互いに一意の類似度に変換することができる.異常値に対して反応の重みを低めに与えている類似度になります.

$$Dise類似度 = \frac{ 2 I }{ A + B+ 2I }$$

Simpson類似度は片方がもう片方を内包する時に1になるのが他と異なる点です.なのでより似ているものにたいして1を与えているような挙動になります.

$$Simpson類似度 = \frac{ I }{ min(I +A , I +B) }$$