-
 @ThothChildren
@ThothChildren
- 2018.5.17
- PV 237
無限の三角関数の和で関数近似する
ー 概要 ー
無限の三角関数の和で関数近似を行う方法について紹介します.ここでは有名なフーリエ級数展開を用いた方法について紹介します.

この章を学ぶ前に必要な知識
条件
- 周期性をもった関数を近似する
- 区間を設ければ周期性のない関数でも可能
- 区間の間連続である必要がある
効果
- 対象の関数f(x)をsinとcosの和で記述できる
ポイント
- 無限級数になるため、通常どれほど展開するか、項数をいくつにするか決めて使う
- テイラー展開のようにある点での展開ではないため、どの点でも値が大きくずれていくことはない
- 条件とポイントを含めてこれらはフーリエ級数展開の特徴を指して説明している
解 説
無限の三角関数の和で関数近似する方法について紹介します.
工学的には信号等に関わっている方は周波数に関連した三角関数の形で関数の和を表現できることは幾らかメリットがありそうです.
今回三角関数による和を求めるにあたって、フーリエ級数展開を使用します. | 無限の三角関数の和で関数近似する |
フーリエ級数展開の式自体の前に特徴を記述しておきます.
ポイント
・sinとcosの和で近似するため、近似後の関数も周期的な関数になります.
・級数展開できる関数f(x)は、ある区間で発散せず、滑らかに連続であることだけです.
・無限級数の近似になるため、実用上はどこかで展開を停止します.
・テイラー展開はある点の周りでの展開でしたが、フーリエ級数展開はそういったことを気にする必要はありません. | フーリエ級数展開の特徴 |
あくまでフーリエ級数展開を使用して関数の近似をするということの紹介を行うため、詳細はwikipedia等を参考にしてください. | 外部リンク フーリエ級数 |
 | フーリエ級数の式 |
上記の式で\(f(x)\)を表現することになりますが、実際に行う計算は、
ひたすら\(a_k\)と\(b_k\)の値を求める作業になります.
この計算は単純で, \(f(t)\)と\(cos(nt)\)または\(sin(nt)\)の積を区間で積分するのみです. | フーリエ級数展開の係数を求める. |
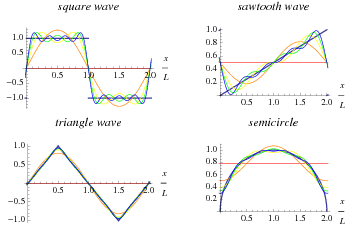 | その他の関数f(x)におけるフーリエ展開例.
先ほど特徴で記述した性質を持つ関数ならどんなものでも展開可能です. |
この章を学んで新たに学べる
Comments


