-
 @ThothChildren
@ThothChildren
- 2018.5.15
- PV 269
制御点で滑らかな関数近似をしたい
ー 概要 ー
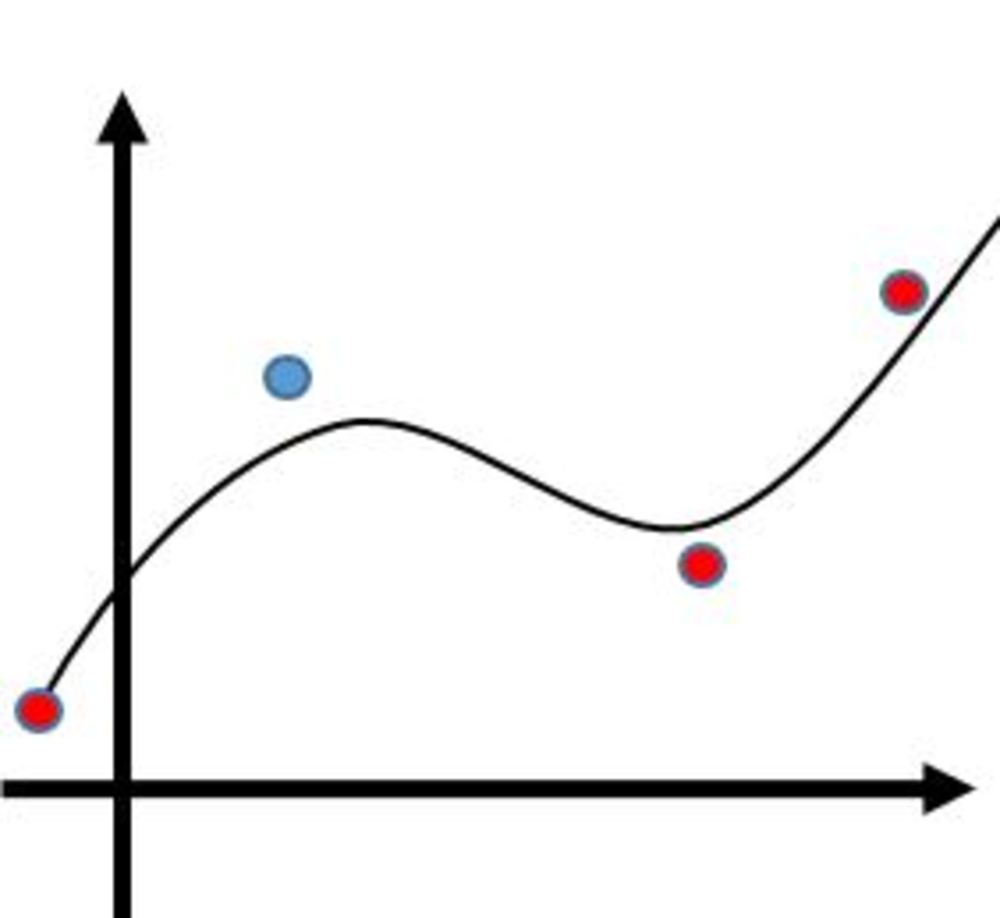
複数の制御点またはデータ点を使って滑らかな関数近似を行う方法について紹介します。ここで紹介するものは点を必ずしも通ることのないものを主に紹介しています。また点列はすでに想定する順番にソートしてありその関数を推定するものとします.
この章を学ぶ前に必要な知識
条件
- 複数の制御点またはデータ点を入力とする
- 与える制御点に前後の関係があることが前提
効果
- それらの点を通る又は点で制御した関数を得られる
- 傾きが滑らかな連続の関数が得られる
ポイント
- ベジェ曲線とBスプライン曲線が有名.ベジェ曲線はスプライン曲線の特殊版.
- ベジェは開始点と制御点によってその制御点の影響度と傾きが決まる
解 説
制御点を用いて全ての点を通る必要はなく関数近似をしたいときの技術についてまとめます.
主にここではベジェ曲線とBスプライン曲線について紹介します.与えられる点列には前後がありその順序に沿って曲線を決定していく.
複数の点を参考にして関数を決定する方法(ガウス過程等)は他にも山ほどありますが、上記の条件を満たすような関数のみを紹介します. | 制御点で滑らかな関数近似をしたい |
1.制御点で曲線の傾きや形を決める | |
1.1.ベジェ曲線 | |
 | ベジェ曲線の図解 |
ベジェ曲線を用いれば直感的に曲線の傾きや形状を制御できるため多くのアプリケーションで採用されています.
ベジェ曲線で両端の制御点を必ず通りますが、その間の制御点はあくまで制御するだけにとどまりそれらを通ることは全く強制されません.
パラメータtを用いてベジェ曲線上の点は表現され0≦t≦1の間をtが移動するときに曲線を描いて開始点から終点までを移動して曲線を描きます.
| ベジェ曲線概要 |
ベジェの詳細については右の参考のリンクにて.
制御点と開始点のなす傾きがそのまま曲線の傾きになるため、複数のベジェ曲線をつなぐ場合は同一点に対応している二つの制御点が一つの直線状に並んでいれば傾きはスムーズにつながります。 | 外部リンク ベジェ詳細 |
1.2.Bスプライン曲線 | |
 | Wikipediaより
Bスプライン曲線図解.
途中の制御点は通っていないことが分かる.
|
Bスプライン曲線はベジェ曲線と並んで頻繁に使用される補間関数の一つです。
Bスプラインではスプライン基底関数の重みによって各点の影響度を決めて足し合わせて曲線を作成します。
下記の数式におけるPは制御点の座標です.
区分的なところでそれぞれ有効になる関数が限られているため、一部を変更しても曲線全体の形状が変わることはありません.
| Bスプライン曲線の概要 |
$$S(t) = \sum_{i=0}^{m-n-2} P_ib_{i,n}(t) $$ | n次のBスプライン曲線.
tはノットと呼ばれる数字列.
単調増加する数列で、階数(1+次数)+制御点数になります. |
1.3.NURBS | |
NURBSはBスプライン曲線を一般化したものといわれます.CAD等ではよくNURBSが実装されているのでそちらも参考にしてください. | NURBSについて |
NURBSは、Bスプライン関数の基底関数が一様に同じであるところが、非一様になっており制御点によって形状が異なります。 | NURBSの特徴 |
この章を学んで新たに学べる
Comments


