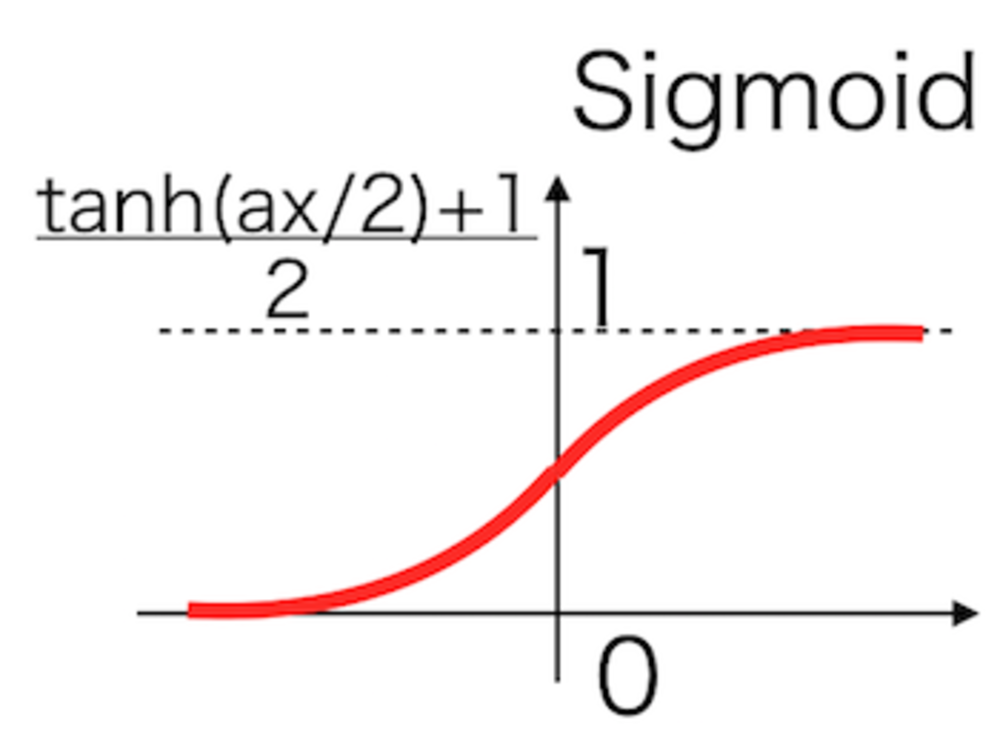
Sigmoid活性化関数

Relu関数等が登場するまで長らく使用されてきた関数. 人間のニューロンを参考に作られた関数で、長らく使用されてきたが、 勾配消失問題の原因となるため、現在は使用されることはない.

$$f(x)=\frac{ 1}{ 1 + e^{ -x } }$$

$$f'(x) = (1- f(x))f(x)$$

シグモイド関数の微分をしたものは、入力xが極端に大きいまたは小さいときに0に近くなってしまい、ほとんど学習が進まなくなることが挙げられます。 また、シグモイド関数の微分は常に1より小さい値しか出さないため、これらの値を掛け合わせるように層を深くしていくと勾配はもっと小さくなっていってしまいます。 層を深くした入力に近いところでは勾配が限りなく0に近くなってしまい、逆誤差伝播がほぼ意味をなさなくなってしまいます。 Reluを使用した場合はこれらの問題が解決されます。