チェビシェフ距離を使う

チェビシェフ距離は、以下のミンコフスキー距離の極限を計算したものに等しい 以下の式で表される

$$ \begin{align} d &= \lim _{{k\to \infty }}{\bigg (}\sum _{{i=1}}^{n}\left|p_{i}-q_{i}\right|^{k}{\bigg )}^{{1/k}} \\ &= \max _{i}(|p_{i}-q_{i}|) \end{align} $$

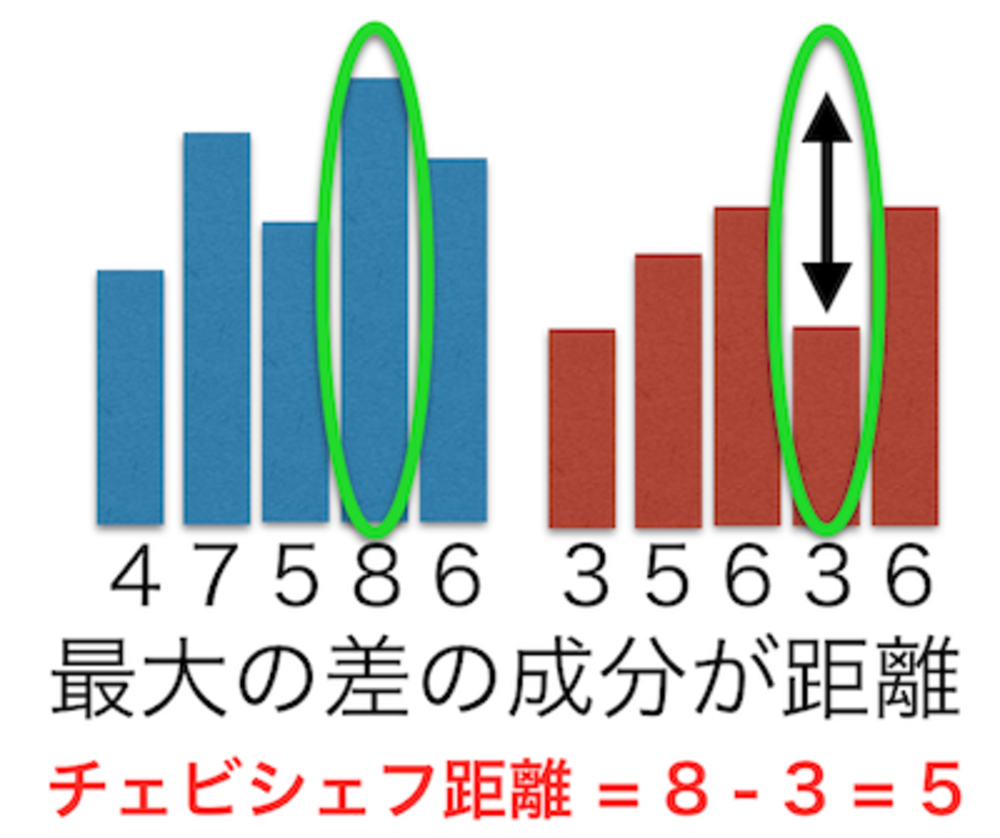
上記のように、チェビシェフ距離は最も差のある要素の差を距離としたものである。 他のL1距離(マンハッタン距離)やL2距離(ユークリッド距離)等と同じように機械学習等の分野で利用されることがある.