-
 @ThothChildren
@ThothChildren
- 2017.9.10
- PV 572
マンハッタン距離を使う
ー 概要 ー
マンハッタン距離は、ある座標系の座標の差を全て足したものとなる.
ユークリッド距離は全ての要素での離れ具合を要約したものだが、マンハッタン距離では一つの要素でも遠ければ遠いと判定される距離となっている.
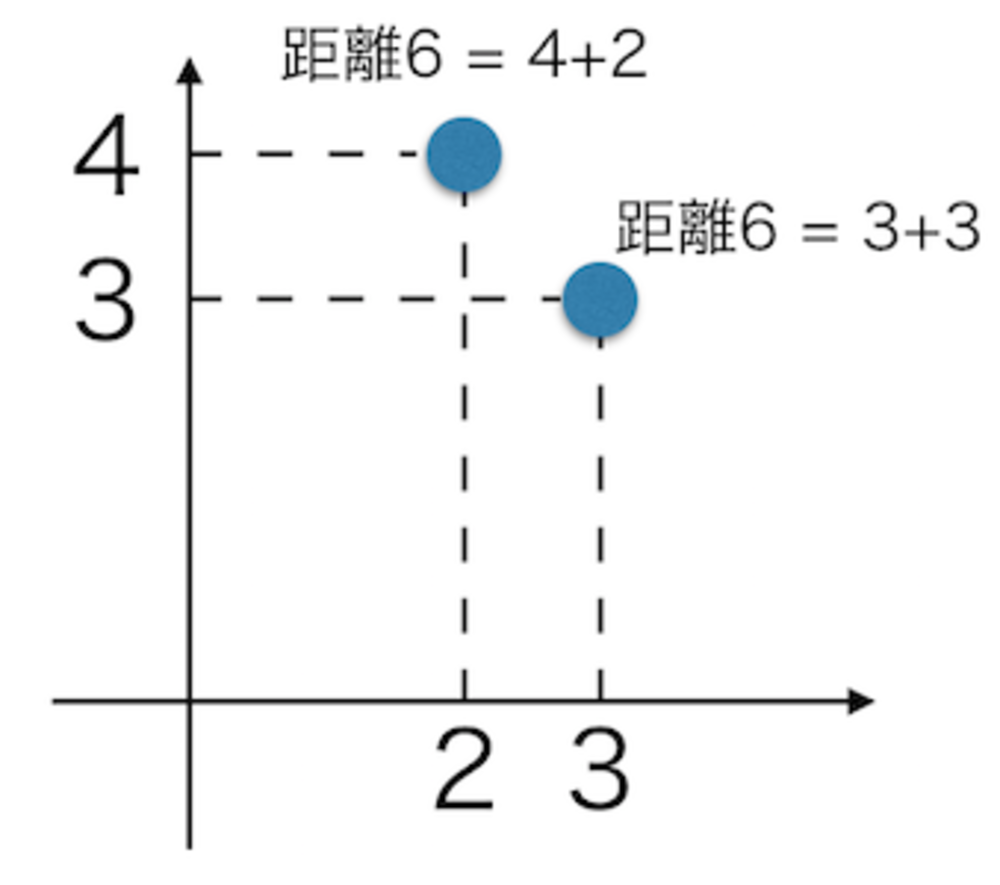
この章を学ぶ前に必要な知識
条件
- 二つの要素数の等しいベクトルが入力
効果
- 各要素の引き算をしたものを合算したものが距離
- 一つの要素でも大きく外れていれば、距離も大きくなる.
解 説
マンハッタン距離は、京都やマンハッタンのように碁盤の目のような道で得られる距離のイメージです。
かならず座標軸と同じ方向に等しくなるため、最短の道が何本か出てきます。 | マンハッタン距離導入 |
マンハッタン距離 dddd は,
d(x,y)=n∑k=1|xk−yk|d(x,y)=n∑k=1|xk−yk|d(x,y)=n∑k=1|xk−yk|d(x,y)=∑k=1n|xk−yk|
と表される。 | 外部リンク マンハッタン距離 |
マンハッタン距離を2次元の場合を考える
二つのベクトル
⃗a=(4,3)a→=(4,3), ⃗b=(1,5)b→=(1,5)
があるときのマンハッタン距離は、
d=|4−1|+|3−5|=5d=|4−1|+|3−5|=5
| マンハッタン距離例 |
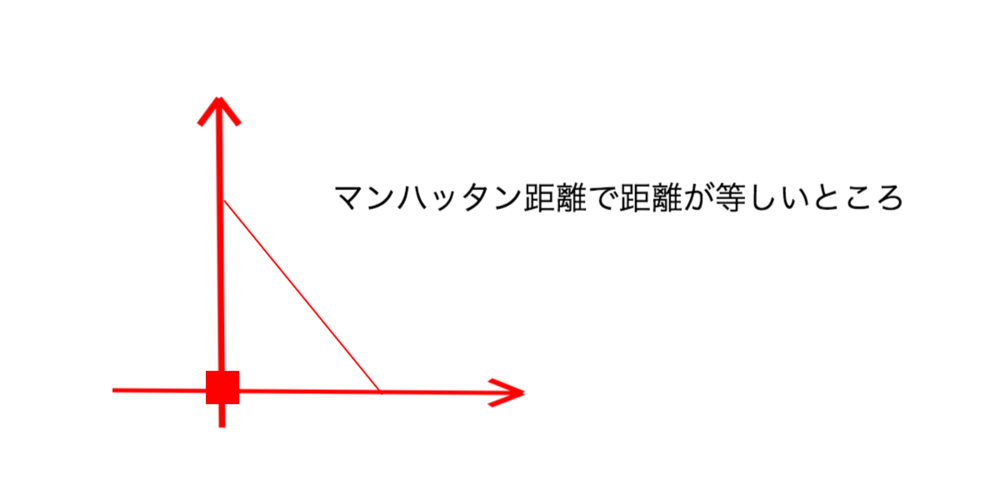 | ユークリッド距離は円状に等距離なところが得られるが、
マンハッタン距離は斜めの直線上に当距離な位置が分布する |
ユークリッド距離と同じくらい有名な距離ですが、どういった違いがあるのでしょうか?
最も簡単な性質上の違いは、多次元の二つのベクトルにおいて100個の要素のうち99個の差が0、一つの要素だけ100の差がある場合などを考えるとわかりやすいです。
・ユークリッド距離では、10
・マンハッタン距離では、100
すなわちほとんど等しいベクトルのときにユークリッド距離は近いものと扱われ、
マンハッタン距離では一つでも大きく外れていれば遠いものとされるということです。 | マンハッタン距離のポイント |
この章を学んで新たに学べる
Comments


