時系列間の類似度計算を選ぶ

時系列データの類似度は、時系列データの分析、分類等で算出する必要がある。 ここでは以下の2つの類似度の計算方法を紹介する.

• CCF(相互相関関数)
• DTW(Dynamic Time Warping/動的時間伸縮法)

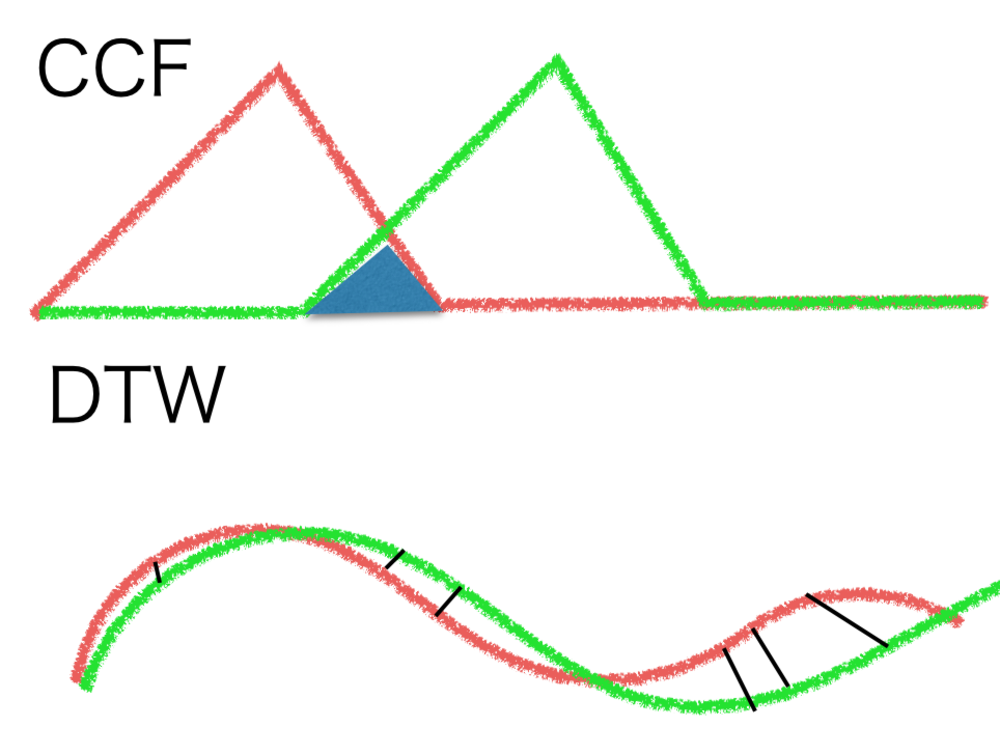
CCFは関数(連続/離散両方)または時系列のデータの類似度を計算することができ、 また、周期の遅れ等を求める際に使われる。 しかし、CCFは周期が伸縮するような時系列データの類似度を計算することには使用できない。

関数の類似度を考えたときにどうしたら似てるかは、 もっとも単純には関数を掛け合わせて積分すればわかりそうだ。 その考え方はCCFのもっとも単純化した例に対応する.

$$(f\star g)(\tau )\ =\int _{-\infty }^{\infty }f^{*}(t)\ g(t+\tau )\,dt,$$

$\tau$ は片方の関数をずらすためにある引数だと思ってください。 例えば $\tau$が0となったとき、それは関数をずらさずに掛け合わせて積分している上の話の例と同じ状況になります。

もし $f$と$g$が同じ関数でありながらわずかにずれているとき CCF定義の $\tau$ を少しずつずらして計算していけば、最も一致するときに CCFの値が大きくなることは想像できる。 その時の $\tau$ が遅れに対応する.

上記の流れは、 離散的な関数にも、またもちろん時系列のベクトルデータに対しても同様に計算することができる。

DTW(動的時間伸縮法)では、周期が一部で遅かったり、早くなっていても 時系列データの類似度を計算することができる.時系列データならどんな対象でも導入できますが、主に音声の時系列データ, 文字列認識等に使用されてます。

Dynamic Time Warpingは波形それぞれの各時間の点同士を総当たりで 求める方法です。 最もそれらしい対応点を探すためのアルゴリズムになります。